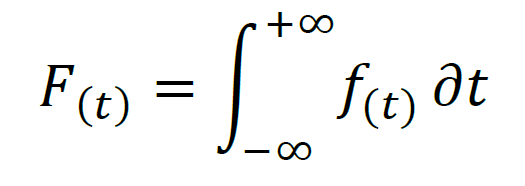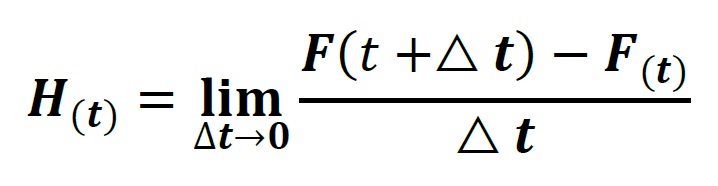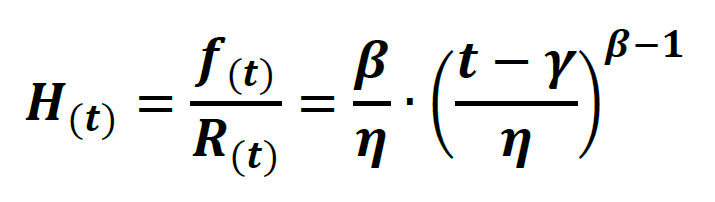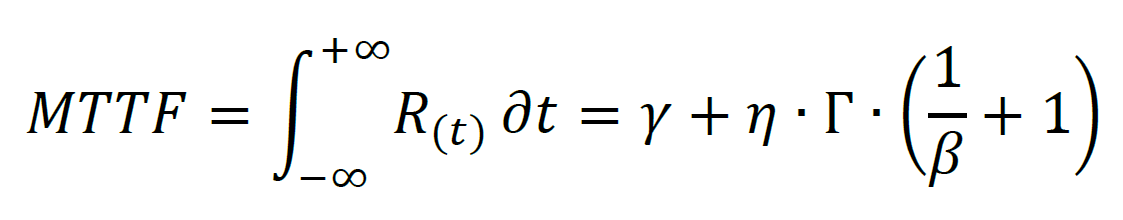Análisis Cuantitativo de Confiabilidad (por la función de distribución estadística de Weibull)
Conceptuación
Por definición técnica, Confiabilidad es la probabilidad de un ítem o sistema, reparable o no, de cumplir una determinada función, primaria o secundaria, durante su tiempo de operación, y según el contexto operacional que él se encuentra. Aún vale se decir que, cuando el sistema es reparable, esa probabilidad es para su primera ocurrencia, teóricamente, así debe ser comprendido.
Es decir, analizarla cuantitativamente significa fundamentalmente calcular esa probabilidad y otros valores, o indicadores numéricos, que esa teoría permite que sean obtenidos. El Análisis de Datos de Vida es el nombre de la teoría, o metodología, utilizada para un análisis cuantitativo de confiabilidad.
Análisis de Datos de Vida Life Data Analysis (LDA)
Para ese artículo, y de forma básica, hacer un análisis de datos vida, significa distribuir los registros temporales de falla que una muestra de ítems o sistemas presentaran en un periodo historial como será demonstrado a seguir:
O sea, es necesario la utilización de una función matemática para se distribuir los registros de fallas, o ocurrencias, observados en un cierto contexto operativo. A partir de ella, los indicadores de confiabilidad, y otros, podrán ser calculados. Existen varias funciones matemáticas para ese tipo de análisis, como:
✓ Función de Distribución de Gauss (Normal);
✓ Función de Distribución de Weibull;
✓ Función de Distribución de Gumbel;
✓ Función de Distribución de Erlang;
✓ Función de Distribución Log-Normal;
✓ Función de Distribución Exponencial;
✓ Función de Distribución Gama;
✓ Etc…
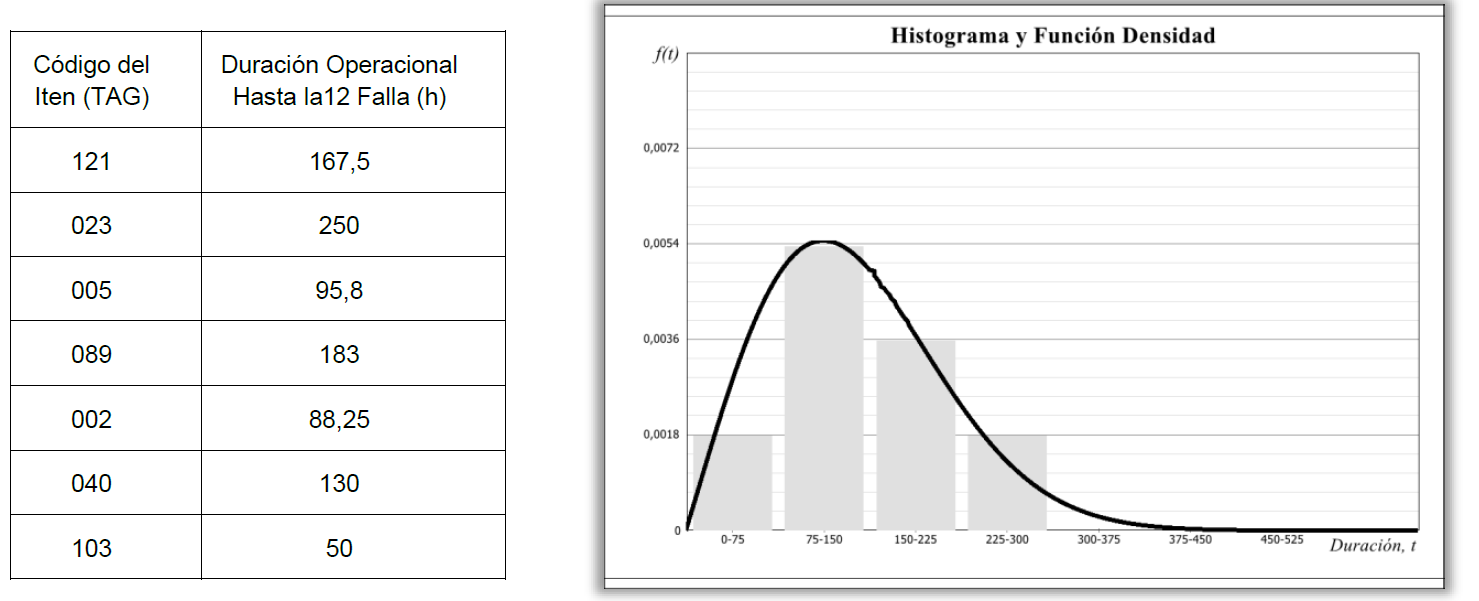
La Función de Distribución de Weibull – se lee Veibul, es la función matemática más utilizada en un análisis cuantitativo de confiabilidad debido a su capacidad de modelación de los datos de una muestra, es decir, la función de Weibull es flexible y no posee una forma única, a revés, ella puede diseñar formas gráficas distintas y de esa manera, puede copiar, o replicar, otras funciones de distribución, como demostradas en la figura 1:
Características de la Función de Distribución de Weibull
Descripta por Waloddi Weibull, un ingeniero mecánico de origen sueca, la función que distribuye los registros temporales de falla es llamada de Función Distribución de Densidades de Probabilidades, o solamente Función Densidad de Probabilidad, o Probability Density Function, PDF, en inglés, cuya estructura matemática de la ecuación es:

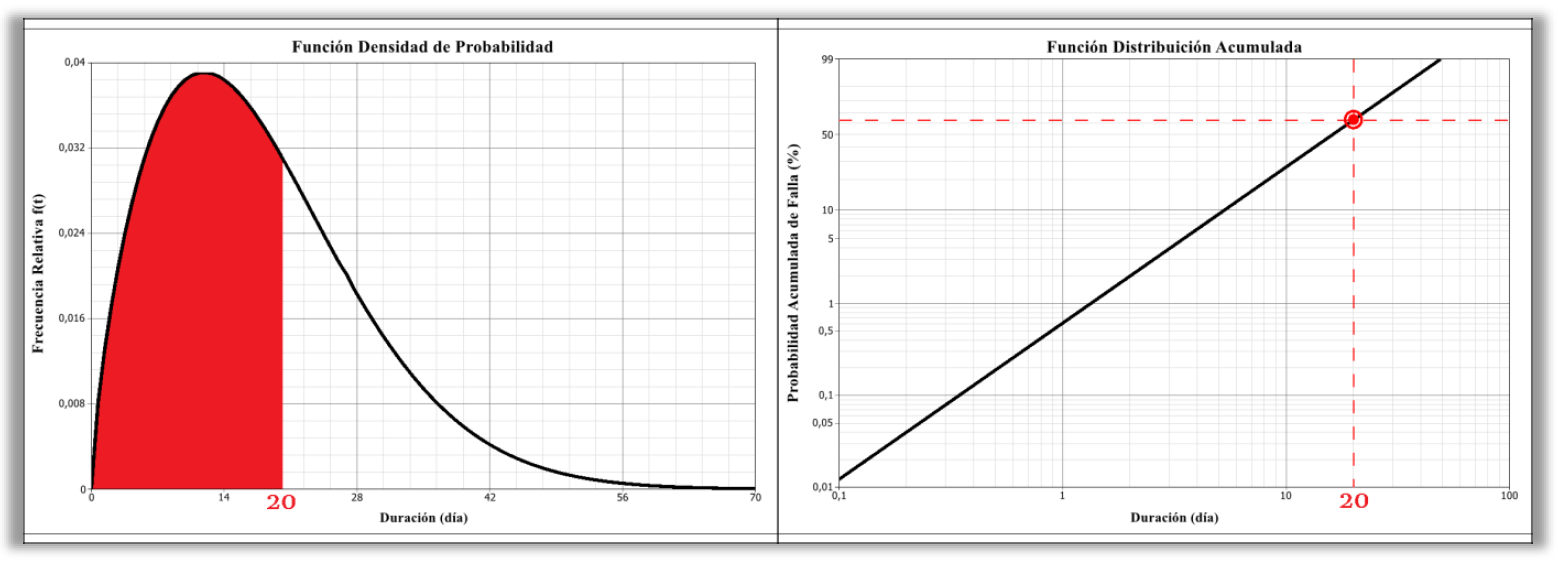
A partir de la integración de la Función Densidad de Probabilidad, PDF, se obtiene la Función Distribuición Acumulada, o Cumulative Distribution Function, CDF, en inglés, y con ella son leídas las probabilidades acumuladas de falla durante el tiempo operativo.
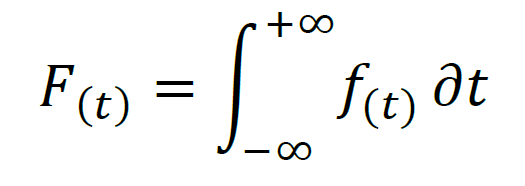
Para la muestra anterior, gráficamente se tendría la curva CDF abajo, o Función Distribución Acumulada:
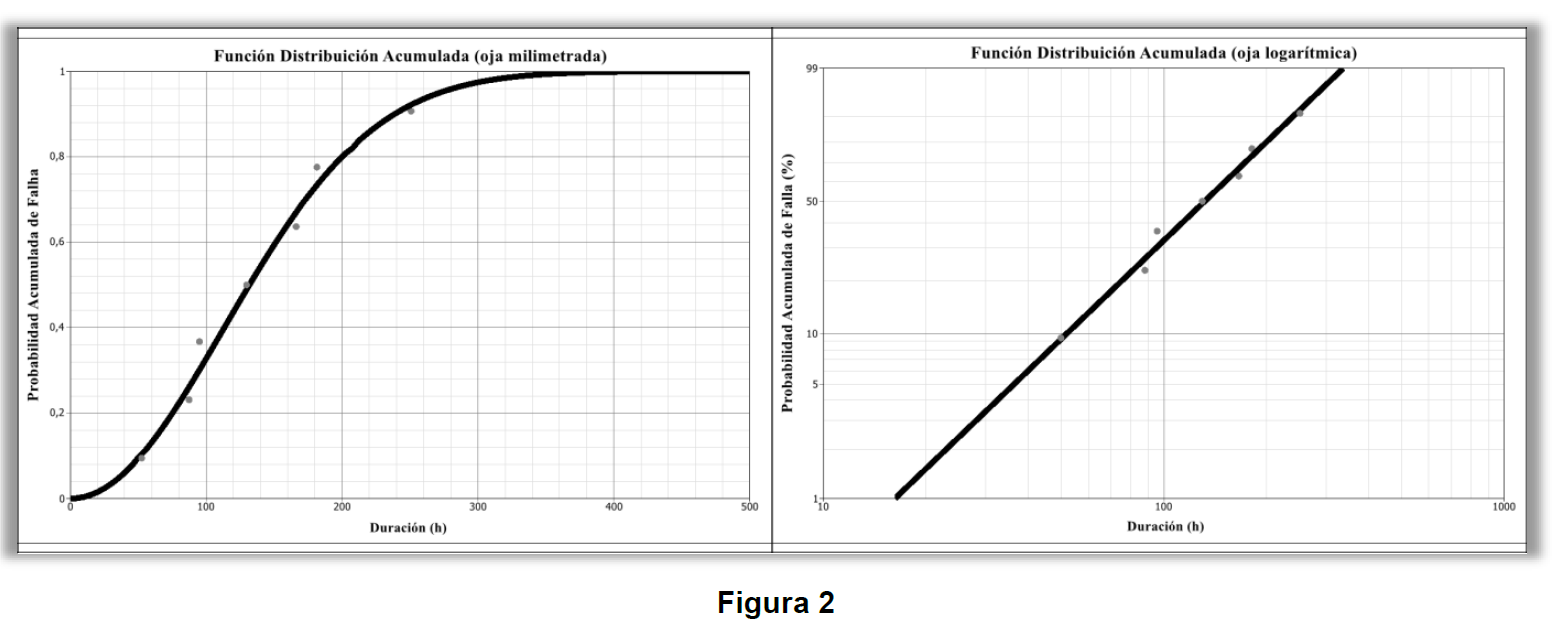
Para el ejemplo, el ítem posee, aproximadamente, la Probabilidad Acumulada de Fallar de 0,8, si él operar hasta 200 horas, es decir que 80% de los ítems idénticos son esperados fallaren hasta 200 horas de operación, con todos ellos operando al mismo contexto operativo y modos de fallas observados y analizados.
El Parámetro de Forma de la Función de Weibull
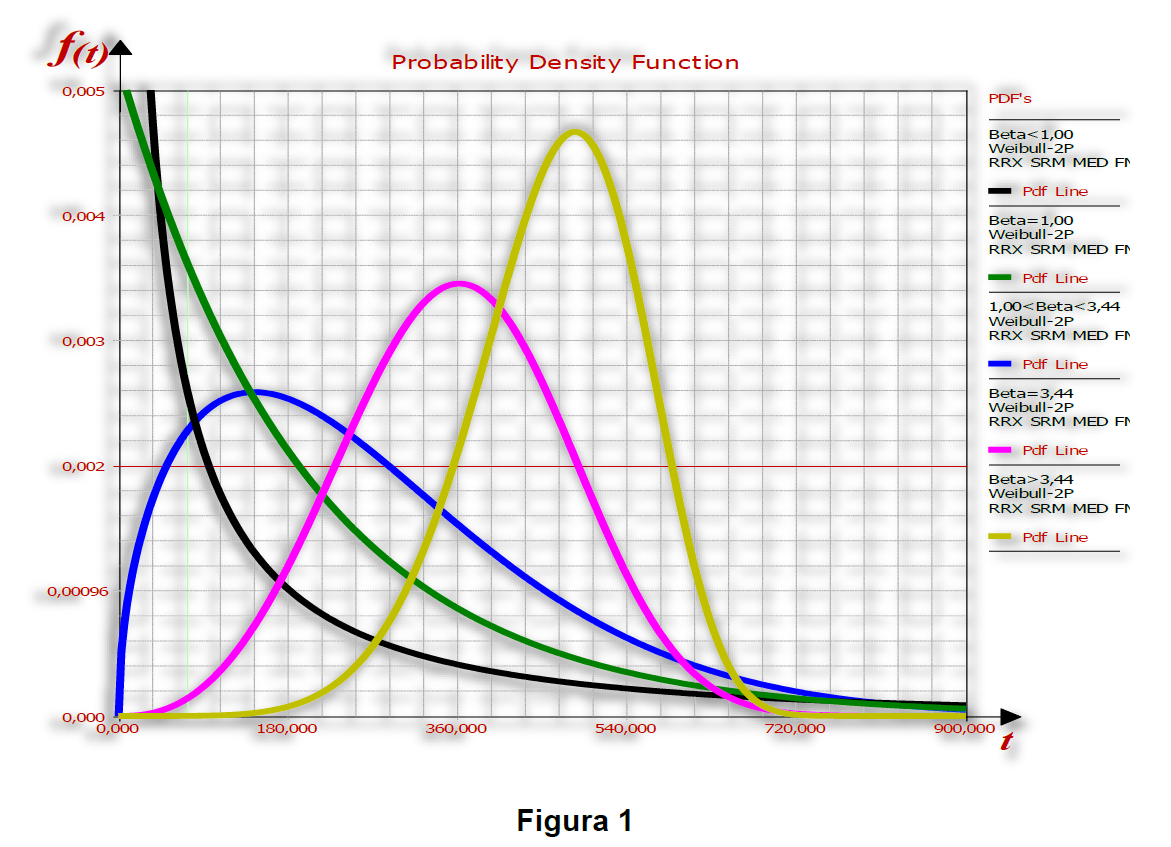
Aquí representado por la letra griega “β”, el parámetro de forma de la función es un número adimensional y “mide” la forma con que los datos se distribuyen gráficamente, o sea, la PDF puede ser simétrica o asimétrica con el tiempo, es decir que se tiene un valor de “B” para cada forma, así como se puede ver en la Figura 1.
Otra observación del parámetro “β”, es que él representa la pendiente de la CDF, o sea, él puede ser calculado por la tangente del ángulo formado por la Función Distribución Acumulada, así como se puede ver en la Figura 2 con β = 2,02. Como ejemplo, observe como queda la forma PDF y respectiva pendiente CDF para 4 valores distintos de “β” en los gráficos que siguen en la figura 3.
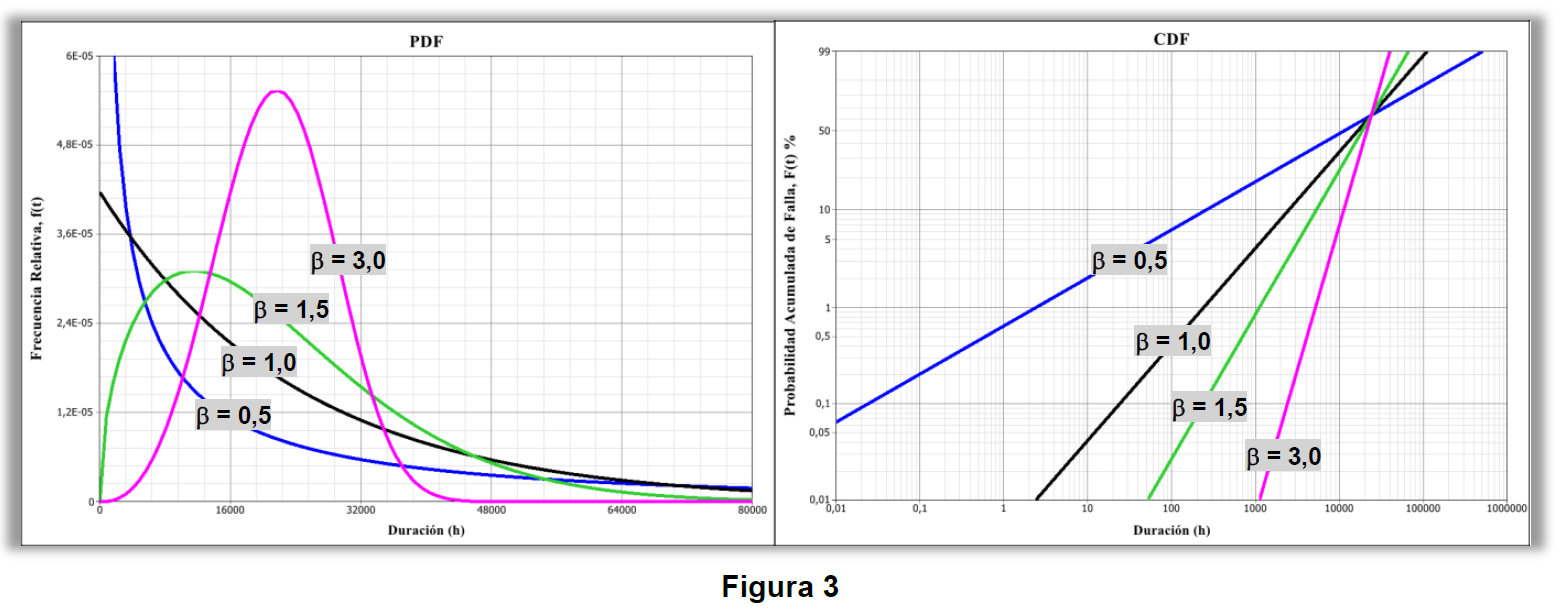
Todos los modelos fueron tomados con el mismo valor del parámetro de escala, η = 1000 días y el mismo valor para el parámetro de posición, γ = 0 día.
Por el gráfico de la PDF se puede ver la capacidad flexible de la función de Weibull. Observe que cuando la muestra calcula un β = 1,0, la PDF queda idéntica a la forma presentada por la función de distribución exponencial, y cuando la muestra calcula un 1,0 < β < 3,0, una asimetría positiva será siempre modelada, así como se hace por una función de distribución Log-Normal. Finalmente, una simetría en la PDF podrá ser observada cuando la muestra de los datos calcular un β ≈ 3,44, y a partir de eso, la PDF queda negativamente asimétrica.
Una otra observación valerosa que se tiene del parámetro de forma de Weibull, es que por él, se puede identificar el comportamiento de falla que el sistema, o ítem, analizado puede estar sufriendo según la muestra de datos analizada. O sea, de acuerdo con el valor calculado para él β, según una muestra, ya se sabe el momento de Curva de la Bañera que ese ítem, o sistema, se encuentra, como demonstrado a continuación.
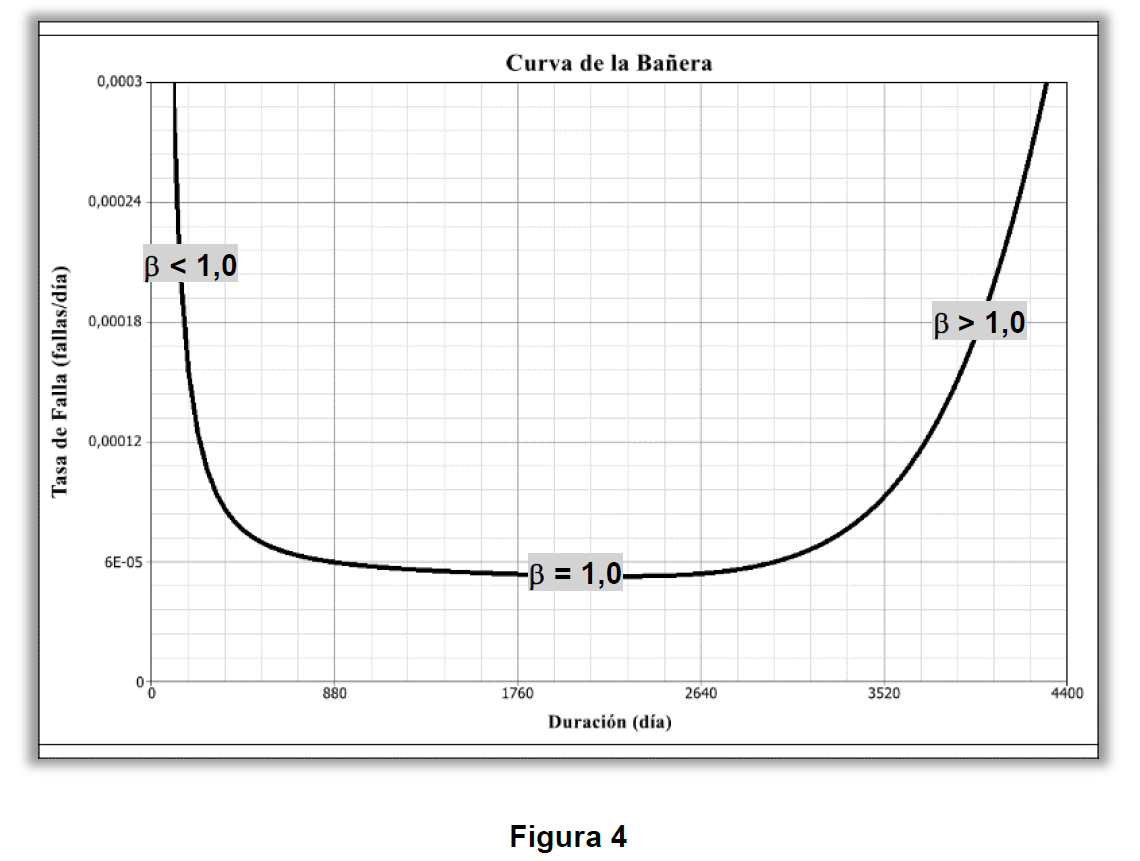
La Curva de la Bañera es construida por la función Tasa de Falla, matemáticamente conocida como función Riesgo – Hazard rate en inglés, que se define como la probabilidad del ítem, o sistema, fallar en el próximo y menor instante de tiempo, dado que hasta el momento, él no ha fallado. Matemáticamente se calcula por la operación matemática del “Lim”, como demonstrado por la formulación que sigue abajo.
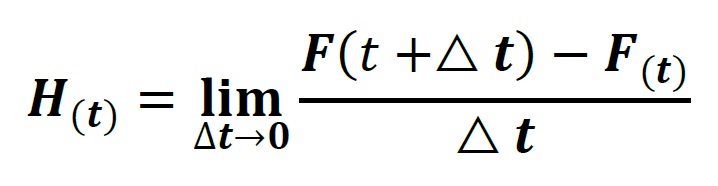
A partir de la función de distribución de Weibull, y sus parámetros, la función Tasa de Falla podrá ser reescrita como sigue.
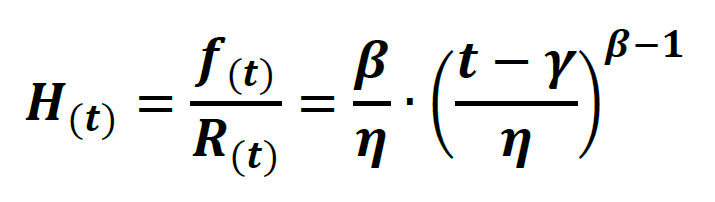
Según la Curva de la Bañera, estadísticamente, una falla puede ser categorizada en hasta 3 comportamientos distintos e independientes. Conocerlos es fundamental y permitirá una gestión más eficiente de los activos.
Fase Niñez: Mortalidad Infantil
Aquí ocurren los modos de falla causados por errores de diseño, como cálculos dimensionales equivocados, calidad material inadecuada o no conforme, etc, pero también por errores durante el proceso de fabricación, como un agujero fuera de la posición o del centro, montaje indebido del producto final, o aún mala instalación, etc. Las tasas de estos mecanismos de falla presentan una disminución con el tiempo de operación. Ese comportamiento de falla se categoriza como Fallas Prematuras.
Fase Madurez: Mortalidad Aleatoria
Aquí ocurren los modos de falla causados por errores durante la operación, como un incumplimiento en el proceso operativo, intencional o no, o una caída en la tensión eléctrica de alimentación, pero también por cuestiones externas, como las climáticas, un relámpago que se cae sobre una máquina o un área de la planta, etc. Las tasas de estos mecanismos de falla presentan un valor constante con el tiempo de operación. Ese comportamiento de falla se categoriza como Fallas Aleatorias.
Fase Vejez: Mortalidad Senil
Aquí ocurren modos de falla causados por degradación material, sea por desgaste, fatiga o corrosión que puede ocurrir, naturalmente, por el uso, o también por estar detenido en el área operacional, o en el almacén (stock). Las tasas de estos mecanismos de falla presentan un aumento con el tiempo de operación. Ese comportamiento de falla se categoriza como Fallas por Degradación (o Desgaste).
El Parámetro de Escala de la Función de Weibull
Aquí representado por la letra griega “η”, el parámetro de escala de la función es un número que posee la misma unidad temporal de la variable aleatoria analizada, por ejemplo, horas, días, ciclos, metros, etc. Cuanto mayor ese parámetro, más “abierta” será el dibujo de la PDF, o sea la escala gráfica “x” queda ampliada, como mostrada abajo por la figura 5.
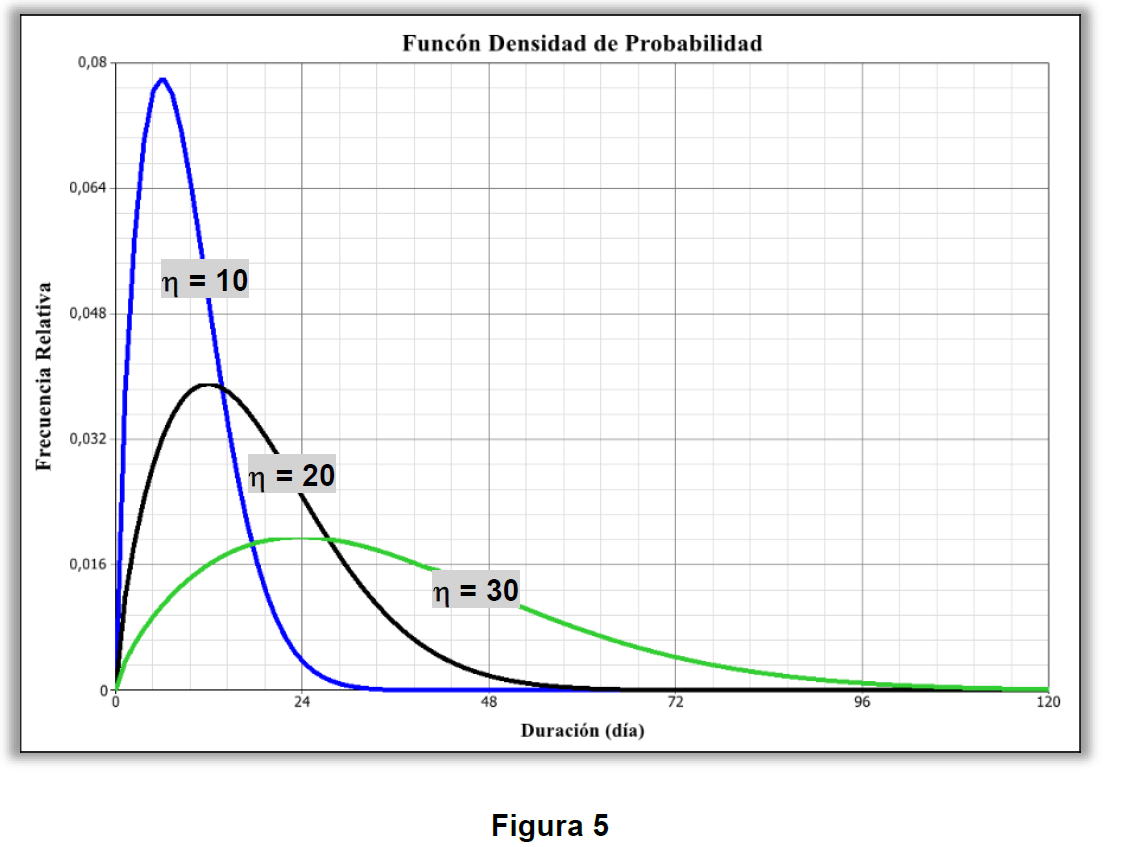
Una observación importante, es que todo parámetro η posee una característica común e idéntica para toda muestra analizada. Esa característica dice que la probabilidad acumulada de falla (o frecuencia relativa acumulada) es siempre 0,632, o sea, 63,2% de los sistemas, o ítems, son esperados fallaren hasta su valor, y justamente por eso, el parámetro de escala, η, también es llamado de “Vida Característica” – F(η)=0,632.
El Parámetro de Localización de la Función de Weibull
Aquí representado por la letra griega “γ”, el parámetro de localización de la función es un número, positivo o negativo, que posee la misma unidad temporal de la variable aleatoria analizada, por ejemplo, horas, días, ciclos, kilómetro, etc. Él indica donde se queda el origen de la función distribución, sea antes o después del cero, como está mostrado en la figura 7, con γ =−10 días (izquierda) y con γ =+10 días (derecha).
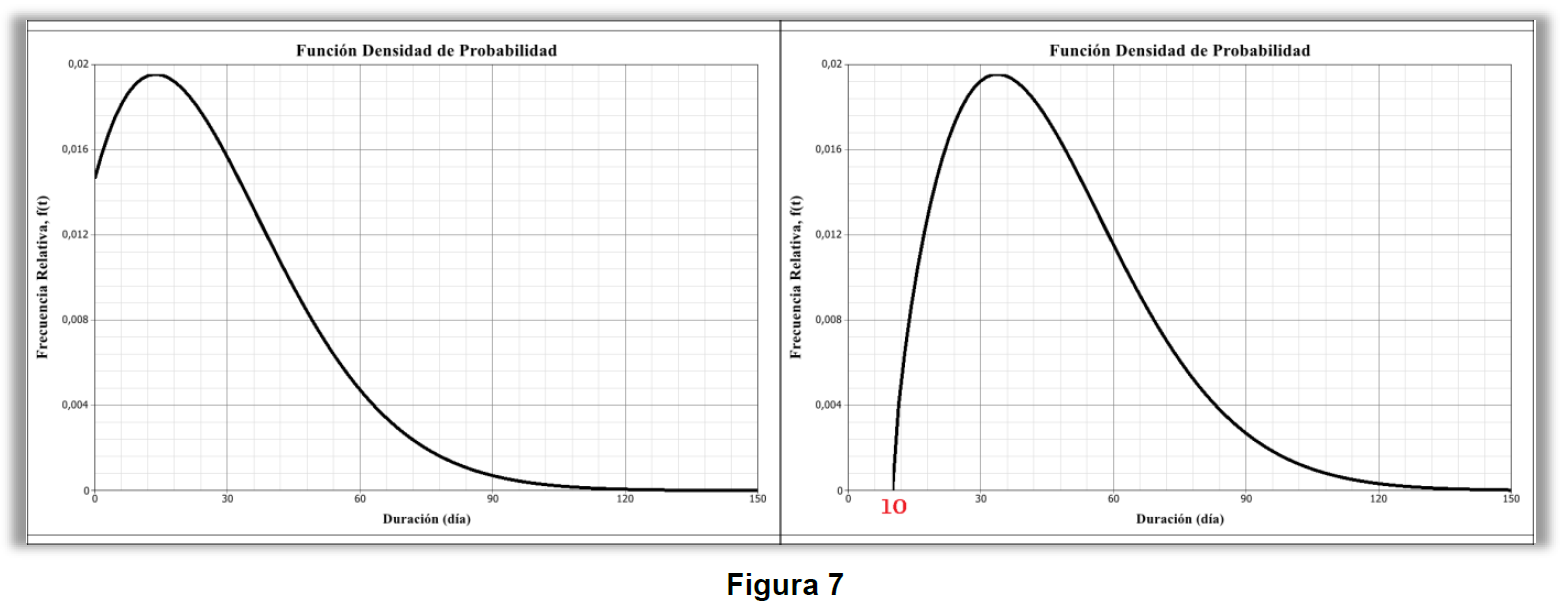
Observe que el gráfico a la izquierda, tenemos un γ negativo en 10 días, es decir, la PDF comienza 10 días antes del día cero, o sea antes del inicio operacional del sistema. Esto significa que la probabilidad de falla del sistema se inicia antes mismo de su operación, sea por errores de diseño, de montaje, calidad, defectos de fabricación, mala instalación, o sea por degradación de él en reposo, como desgaste o corrosión.
En el gráfico a la derecha, tenemos el escenario revés, es decir, un γ positivo en 10 días, o sea, en ese caso, la PDF comienza después de 10 días del inicio operacional del sistema. Inmediatamente podemos creer que los modos de fallas ocurrirán por desgaste, fatiga o corrosión solo después de los 10 días de operación.
Una vez comprendido el dicho arriba, será fundamentalmente necesario validar el modelo de distribución utilizado con el contexto operacional real, es decir, ¿cuál comportamiento de falla está ocurriendo en campo?
El desplazamiento γ también produce efecto sobre la función de Confiabilidad del ítem, o sistema, como se puede ver en la ecuación de Weibull, y los respectivos gráficos, que siguen abajo.
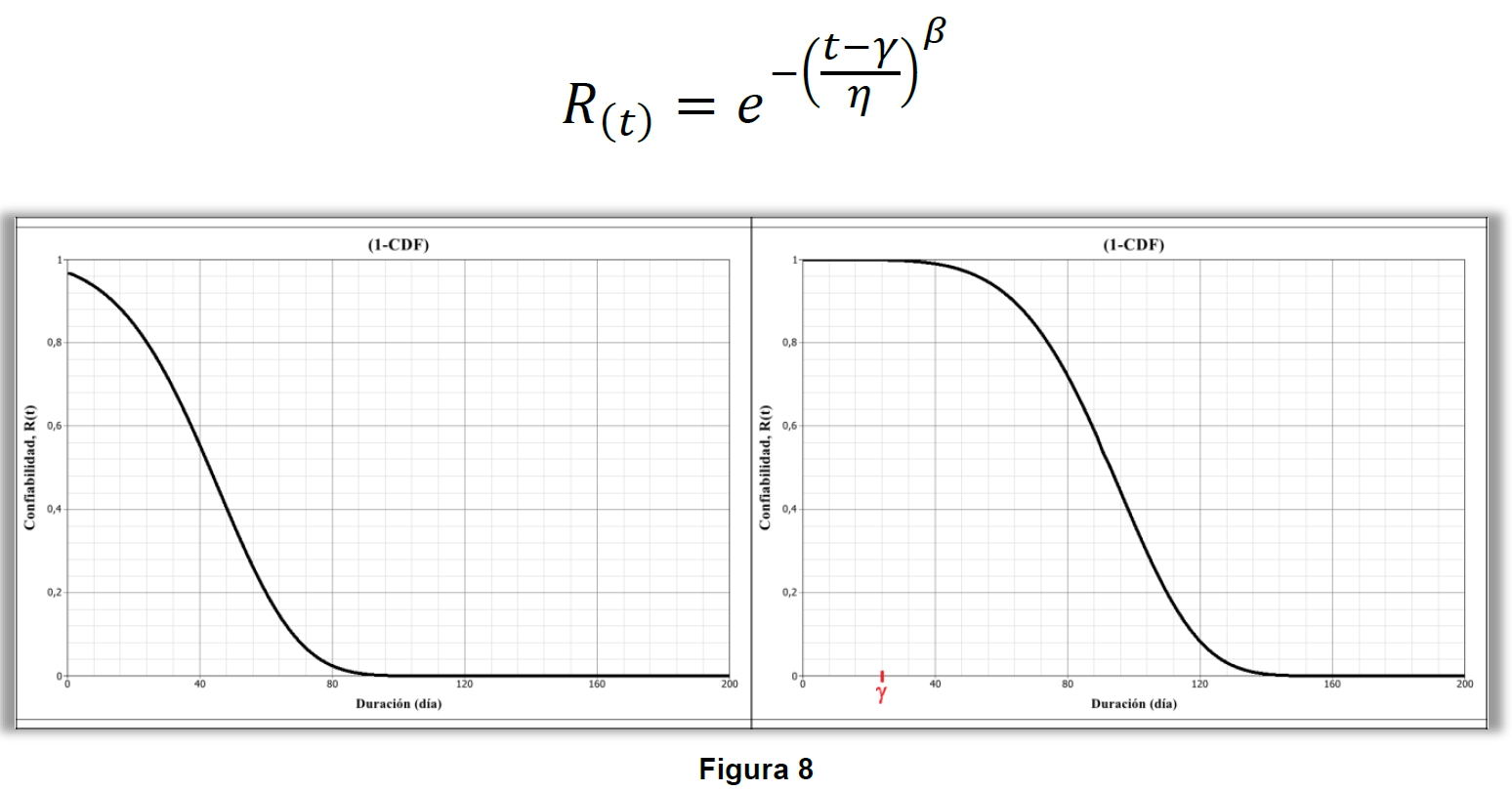
El gráfico a la izquierda posee un γ negativo en donde se observa que la Confiabilidad es menor que “100%” a la origen operacional, o sea, en cero días, y el gráfico a la derecha posee un γ positivo en donde se observa que los “100%” de Confiabilidad comienza a caer después de γ días.
Finalmente, el último concepto de Confiabilidad demostrado en ese artículo, y a partir de los parámetros de la función de Weibull, es la expectativa de vida del ítem o sistema que se obtiene con el punto medio de la distribución, o sea, la vida media o Mean Time To Failure en inglés.
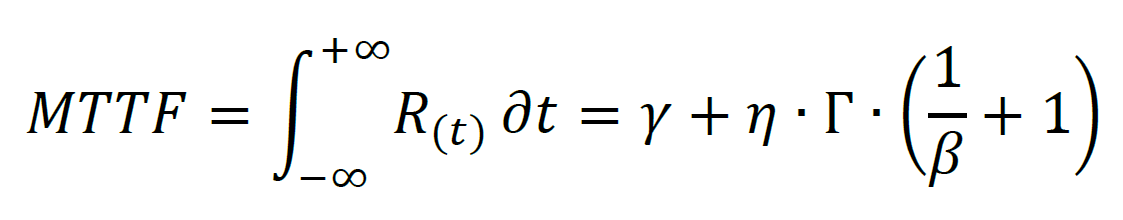
Nota Conceptual Importante:
Un análisis de datos de vida utilizase de modelos matemáticos como la función de distribución de Weibull que calcula el MTTF que es la medida media de la función para un ítem, o sistema no-reparable. La medida MTBF se refiere a la vida media de un sistema reparable, y por eso calculada por otras metodologías, a saber:
1. RGA (Reliability Growth Analysis) Utilizada para los análisis de Monitoreo de la Confiabilidad de productos en desarrollo, y/o también para activos (sistemas reparables) en campo (en uso);
2. RAM (Reliability, Availability and Maintainability Analysis) Utilizada para los análisis y simulación de la Disponibilidad de los activos físicos (sistemas reparables) en campo (en uso).
A continuación, sigue un ejemplo de aplicación con uso de la función de distribución de Weibull apoyada por el software R4All*
(*) Reliability For All
Estudio de Caso con aplicación Weibull
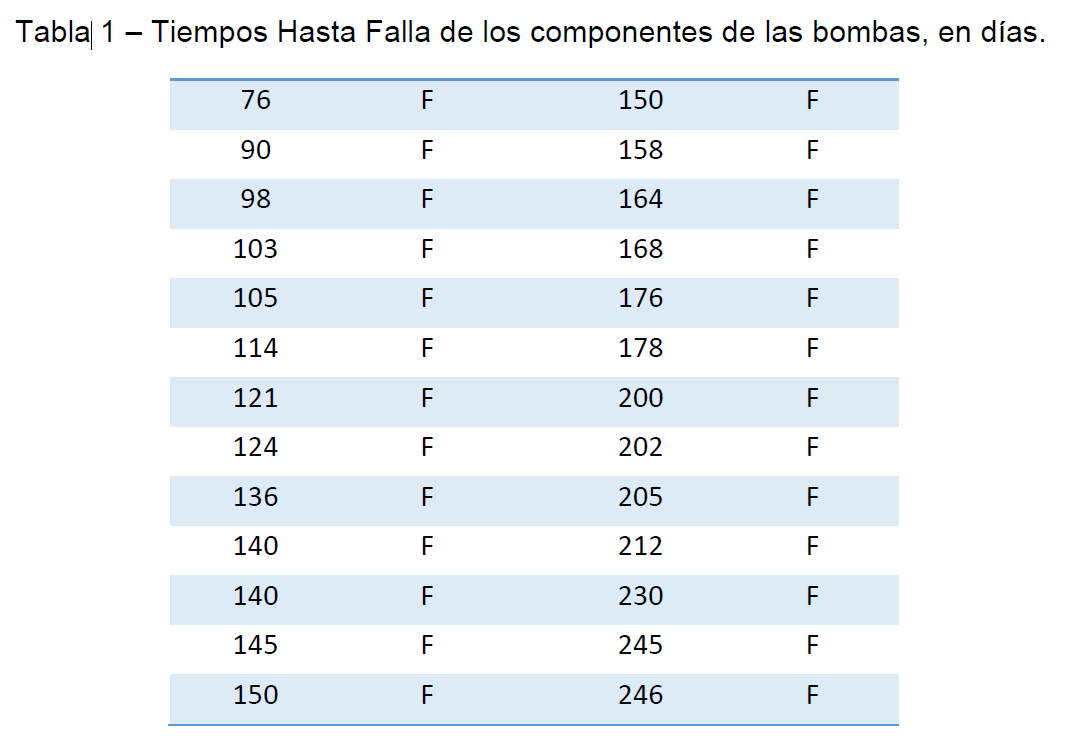
Una determinada organización se utiliza de bombas hidráulicas en las líneas de montaje de su proceso de producción, además de otros tipos de equipos. Después de un análisis FMEA de ellas, se concluyó que el modo de falla de «rotura de componentes» era uno de los más críticos para la bomba porque detienen la operación de ellas, y por eso, impactan en el proceso. A partir de una evaluación del mantenimiento, se pudo identificar que esa rotura ocurre por el desgaste del componente de la bomba. La tabla 1 abajo, contiene los datos completos – Time To Failure, de estos modos de fallas durante, aproximadamente, 1 año de operación.
Además de los datos arriba, un grupo de 10 bombas, que había estado operando durante 180 días continuos, no habían fallado hasta entonces. La figura 9 se observa el gráfico de la Probabilidad Acumulada de Falla de la bomba, por rotura de componente, y según esa muestra de datos completos y censurados a la derecha – estos también llamados de Suspensiones.*
Nota Conceptual Importante:
Cuando la muestra de datos de vida es compuesta por Datos Completos y Censurados, se recomienda el uso del Estimador de la Máxima Verosimilitud (MLE) para la estimación de los parámetros de la función de distribución estadística elegida.
* Dato Censurado a la Derecha se refiere a la duración de tiempo operacional en que la falla aún no se ha ocurrido.
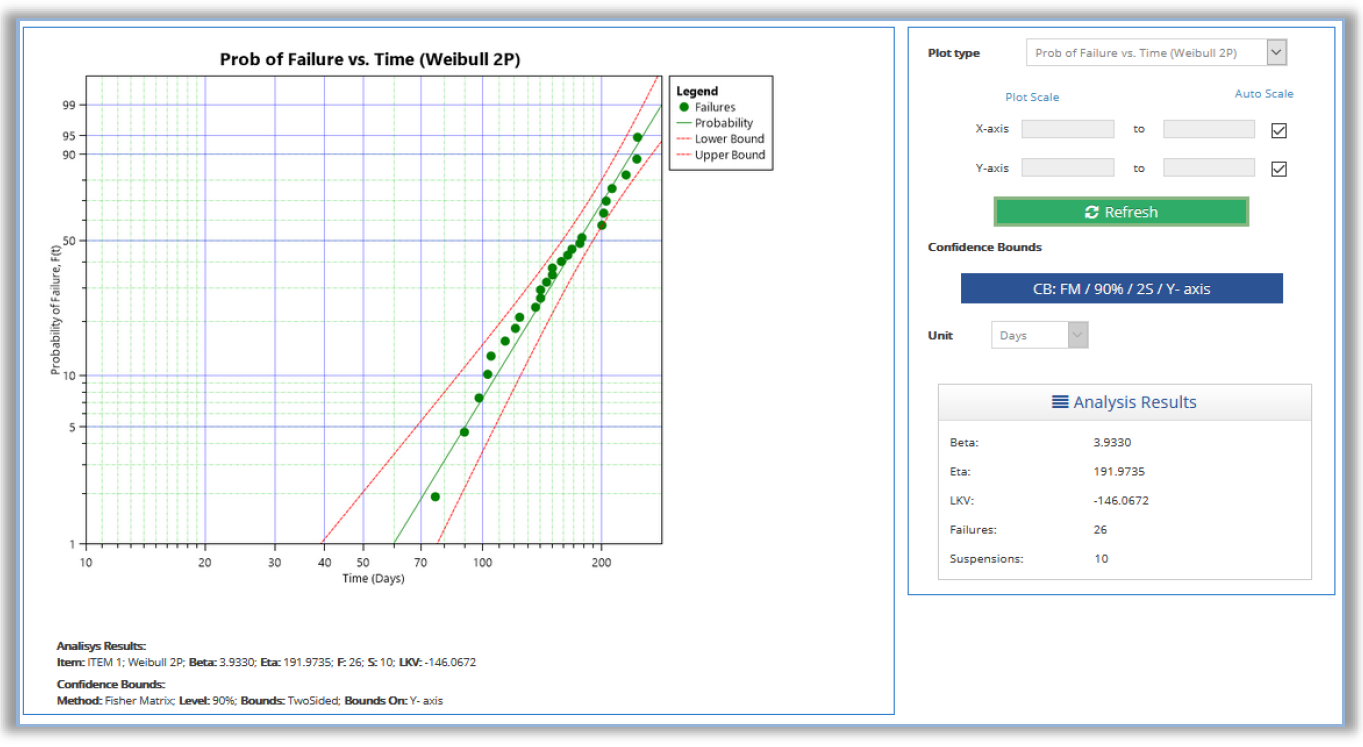
En esa tela, el R4All demuestra que fueran analizados 26 Datos Completos y 10 Datos Censurados a La Derecha para una función de distribución (PDF) de Weibull que ha generado un β de 3,933 y un η de 191,9735 días. Es decir, por el β calculado, el modo de fallar por rotura se confirma, estadísticamente, por desgaste, fatiga o corrosión, y que 62,3% de estos componentes son esperados fallaren (por rotura) en hasta casi 192 días.
Ahora que se conoce la curva que tiende la Probabilidad Acumulada del componente de la bomba fallar, por rotura debido al desgaste, la gestión del mantenimiento de esa organización decide por realizar un reemplazo preventivo de ese componente, para que, de esa forma, se pueda evitar la parada de la bomba y consecuente pérdida de producción.
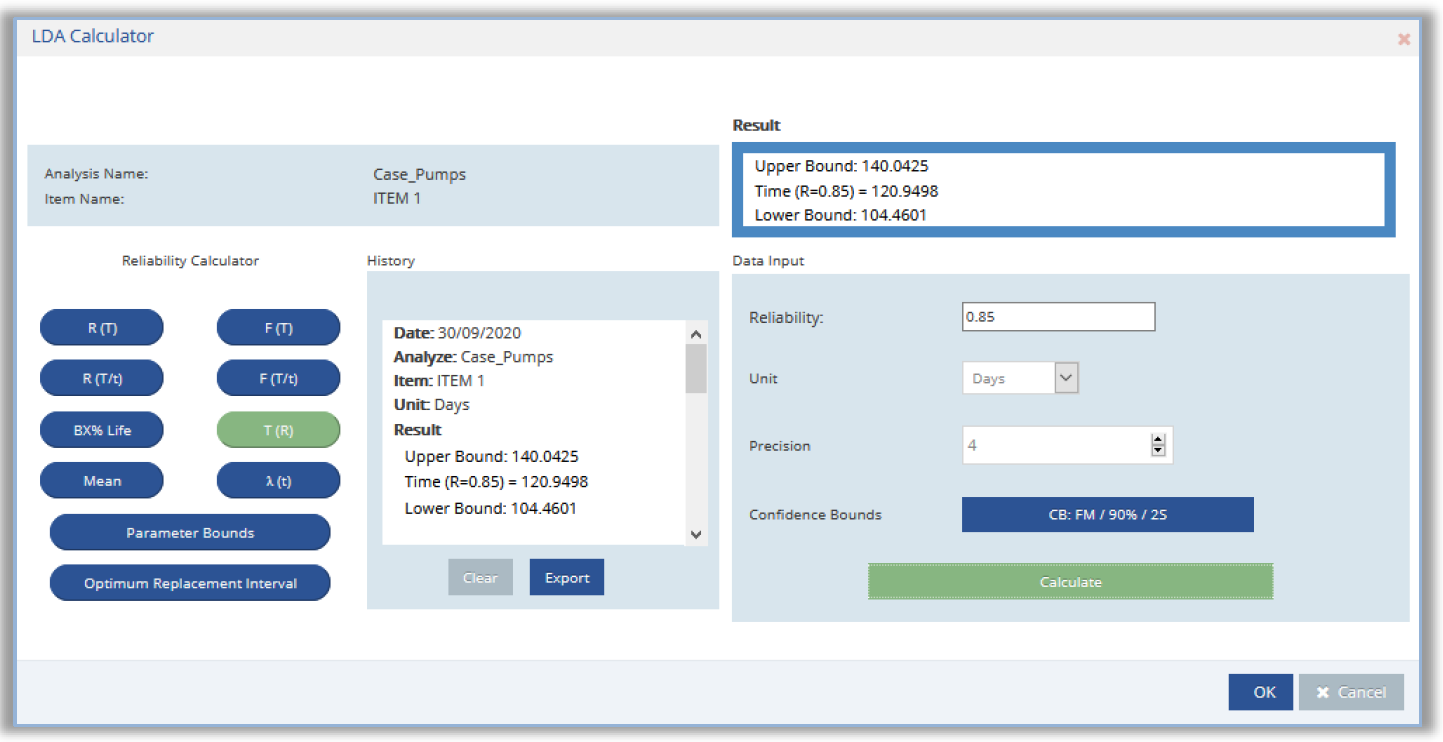
Para eso, fue definido se realizar estos reemplazos preventivos cuando el componente “calcular” una Confiabilidad de 85%, o sea, la Probabilidad Acumulada del componente fallar, por rotura, es de 0,15, o 15% de ellos podrán venir a fallar.
El tiempo, o frecuencia, para ese reemplazo preventivo, se quedó calculado en aproximadamente 121 días y con el debido margen de error de 90% de certeza, o confianza, o sea, entre 104 días hasta 140 días, ese reemplazo deberá ser hecho.
Debido la criticidad del componente, y justo por eso, se garantizar un menor riesgo de fallar, aún con más certeza, 95%, se decide reemplazarlos, con 104 días – poco más de 3 meses de operación.
La figura 9 abajo, se demuestra ese cálculo en el software R4All.
Ese y otros casos de Confiabilidad son transmitidos en los eventos producidos por la Consultoría Compass.
¡Contactenos!