Conceitos de Confiabilidade
Características da Distribuição Weibull
A distribuição Weibull, devido ao nome do inventor Waloddi Weibull, é usada extensivamente em engenharia da confiabilidade devido a sua versatilidade e simplicidade.
Uma distribuição é definida matematicamente por sua equação de PDF (Probability Density Function). Existem outras formas de expressar a distribuição Weibull, porém sua expressão geral é a da distribuição Weibull de três parâmetros, é dada pela seguinte expressão:
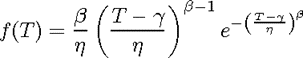
Onde:
![]()
- ß é o parâmetro de forma, conhecido também como inclinação da distribuição Weibull
- h é o parâmetro de escala
- g é o parâmetro de posição
Frequentemente, o parâmetro de posição não é utilizado, e o seu valor pode ser considerado como zero. Neste caso, a PDF se reduz para distribuição Weibull de dois parâmetros.
A distribuição Weibull também pode ser reduzida à sua forma de um parâmetro. Esta de fato, toma a mesma forma da PDF Weibull de dois parâmetros, a única diferença é que o valor de b é suposto de antemão. Esta suposição significa que somente o parâmetro de escala precisa ser estimado, possibilitando uma análise com poucos dados. Recomenda-se que ao fazer isso tenha-se uma estimativa muito boa e justificável para b, antes de usar a distribuição Weibull uni-paramétrica na análise.
Dependendo dos valores dos parâmetros, a distribuição Weibull pode ser usada para modelar uma variedade de comportamentos que envolvam vida. Um aspecto importante da distribuição Weibull é como os valores do parâmetro de forma (b) e de escala (h) afetam as características da distribuição, como a forma da curva da PDF, da confiabilidade e da taxa de falhas.
Parâmetro de Forma – ß
O parâmetro de forma, b, é igual à inclinação da reta em um gráfico de probabilidade utilizando escala logarítmica. Diferentes valores para o parâmetro de forma indicam efeitos no comportamento de vida. De fato, esta distribuição toma a expressão de outras distribuições estatísticas dependendo do valor de b. Por exemplo, quando b=1, a PDF Weibull de três-parâmetros se reduzirá à distribuição exponencial de dois-parâmetros. O parâmetro b é um número puro, isto é, adimensional.
A figura 1 mostra o efeito dos diferentes valores do parâmetro de forma, b, na forma da PDF (mantendo constante o g). Pode-se notar na Figura 1 que a forma da PDF pode tomar uma variedade de formas baseado no valor de b.
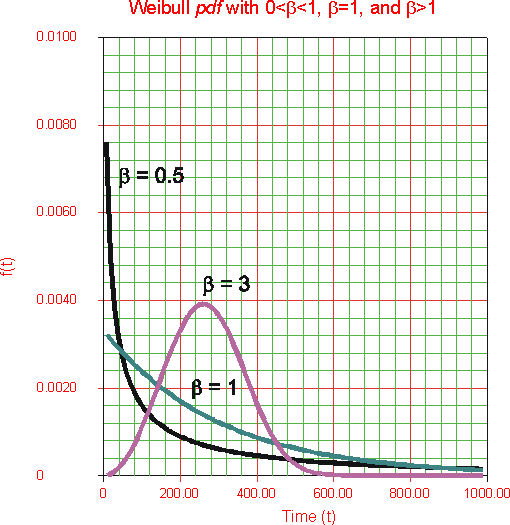
A Figura 2 mostra como a inclinação do gráfico de probabilidade Weibull muda com o b, com os modelos representados pelas três linhas com o mesmo valor de h.
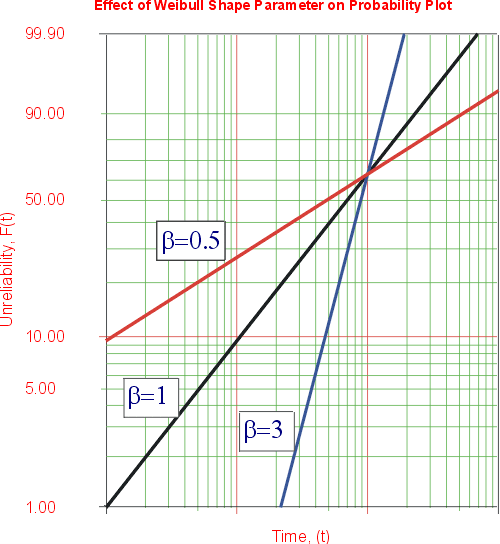
Outra característica da distribuição onde o valor de b tem um efeito distinto é a taxa de falha. O gráfico seguinte mostra o efeito do valor de b na taxa de falhas da distribuição Weibull.
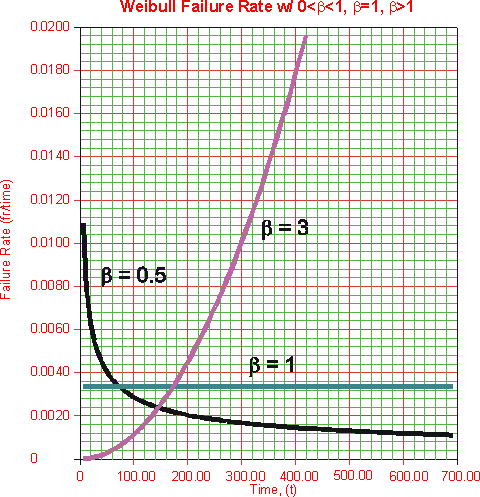
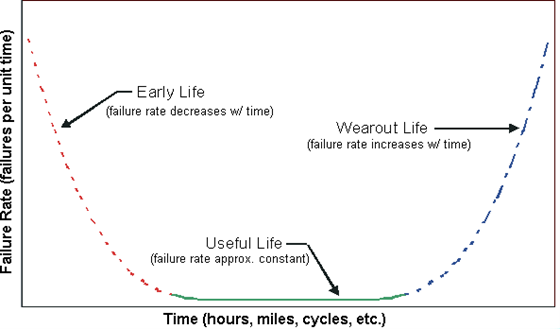
Este é um dos aspectos mais importantes do efeito de b na distribuição Weibull. Como é indicado pelo gráfico, as distribuições Weibull com o b<1 têm uma taxa de falha que diminui com tempo, conhecida também como falha infantil ou prematura. As distribuições de Weibull com o b próximo de ou igual a 1 têm uma taxa de falha razoavelmente constante, indicando a fase de vida útil ou de falhas aleatórias. As distribuições de Weibull com o b>1 têm uma taxa de falhas que aumenta com o tempo, conhecido também como falhas de desgaste. Estes betas abrangem as três fases da “clássica curva da banheira”. A distribuição Weibull mista com a uma subpopulação com o b<1, uma subpopulação com o b=1 e uma outra com o b>1, teria um gráfico de taxa de falhas que fosse idêntico à curva da banheira. Um exemplo de uma curva da banheira é mostrado na Figura 4.
Parâmetro de Escala, h
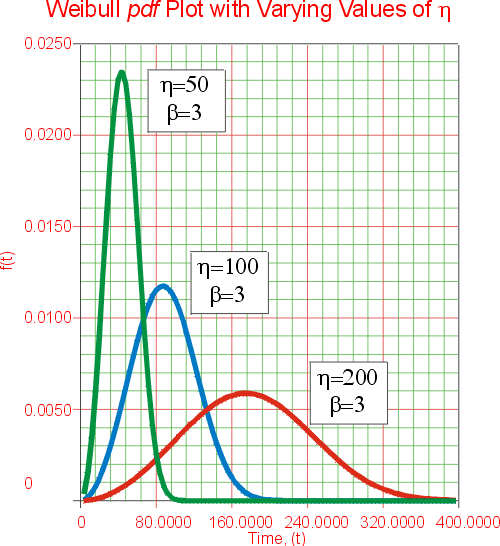
Uma variação no parâmetro da escala, h, tem o mesmo efeito na distribuição que uma mudança de escala na abscissa. Aumentar o valor de h, mantendo constante o b tem o efeito de esticar para fora da PDF. Desde que a área sob uma curva da PDF é um valor constante, o “pico” da curva da PDF. diminuirá também com o aumento de h, como indicado na Figura 5.
- Se h é aumentado, enquanto b e g são mantidos constantes, a distribuição começa a se estender, esticar para direita e sua altura diminui, ao manter sua forma e posição.
- Se h é diminuído, enquanto b e g são mantidos constantes, a distribuição começa se estreitar para dentro, para esquerda (isto é para sua origem ou para 0 ou g), e aumenta sua altura.
- h tem a mesma unidade que T, tal como horas, milhas, ciclos, atuações,etc.
Cálculos Importantes com a Distribuição Weibull
A função densidade de probabilidade pode ser utilizada para se chegar a cálculos comumente usados em confiabilidade, tais como:
- a função de confiabilidade;
- a taxa de falhas;
- a mediana;
- o tempo médio entre falhas.
As equações para estas funções da distribuição Weibull de três-parâmetros são apresentadas abaixo.
As substituições apropriadas para obter as outras formas, tais como a forma de dois-parâmetros onde g=0, ou a forma de um-parâmetro onde b é uma constante, podem facilmente ser calculadas.
A função de Confiabilidade da distribuição Weibull é dada por:
![]()
A função Taxa de Falha da distribuição Weibull por:
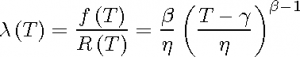
O tempo média de vida, ou MTTF, é dado por:
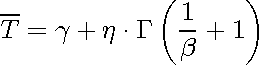
onde G(*) é a função Gamma. A função Gamma é definida por:
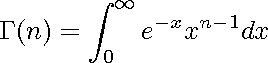
E por fim, a equação para vida mediana, ou vida B50, da distribuição Weibull é dado por:
![]()
Exemplo de Aplicação:
Uma linha de montagem utiliza bombas hidráulicas no seu processo de produção, além de outros tipos de equipamentos. Após uma análise FMEA da planta, concluiu-se que o modo de falha de “quebra da bomba” era um dos mais críticos em termos de ocorrência e efeito, e tinha potencial de levar toda a operação a parar. Também se notou que este modo de falha era devido ao desgaste dos componentes da bomba. A Tabela 1 abaixo contém os dados de falhas dessas bombas para um período de cerca de um ano de operação.
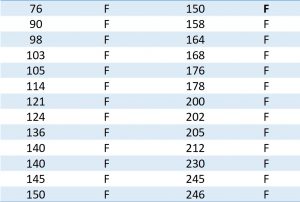
Um grupo de 10 bombas, o qual vinha operando há cerca de 180 dias, não apresentou falhas até então. Abaixo na Figura 6 temos o gráfico da probabilidade de falha obtida para esse espaço amostral.
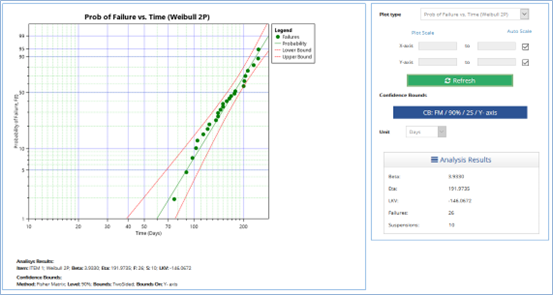
Neste caso, os tempos de operação das bombas que não falharam foram considerados na análise, como censuras à direita (suspensões). Para realizar as trocas preventivas das bombas com cerca de 15% de probabilidade de falha, calculou-se qual o tempo de operação em que a confiabilidade das bombas fosse igual a 85%, como mostra a Figura 7.
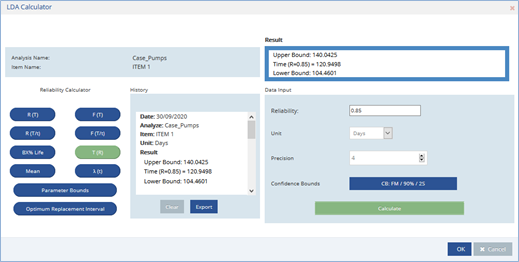
Foi determinado que a troca preventiva das bombas será realizada a cada 120 dias.
——-
Referências:
- Reliability HotWire – The eMagazine for the Reliability Professional.
- Reliability4All – Reliability Engineering Platform | Reliability4All

